| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 쳇지피티
- 에이전트 ai
- 웨크롤링
- react agent
- AI 에이전트
- 책임분리
- 12factorapp
- chatGPT
- agentic ai
- LangGraph
- java17
- temurin
- AI
- 티스토리챌린지
- 오블완
- xmlschema
- Python
- chaosengineering
- 클라우드네이티브
- MSA
- JSON
- ci_cd
- 카나리배포
- web crowling
- 티어구조
- 3티어아키텍처
- LLM
- 포트바인딩
- AI Agent
- API
Archives
- Today
- Total
Nacho
(Python) 평균 추청과 신뢰구간 (모평균 추청, 중심극한정리) 본문
반응형

예제로 이해해 보자.
- 목표
- 주사위의 표본을 달리하여 표본 평균을 구하고 모평균과 비교해 보자.
- 표본 평균이 정규부포를 따르는지 확인해 보자.
우선 우리가 알고 싶은 것이 무엇인지 정확히 이해해야 한다.
💡 우리의 목표 : 직접 주사위 30000개를 굴려서 평균을 구할 수 없기 때문에 주사위를 조금만 굴려서 대충 신뢰할만한 표본의 평균값을 구하고 싶은 것이다.
하지만, 우선 답은 알아야 문제를 잘 풀었는지 알 수 있으니 모평균(모집단의 평균 = 30000개의 주사위 값 평균)을 구해보자.
import random
dices_30000 = [random.randrange(1,7) for _ in range(30000)]
print(round(sum(dices_30000)/30000,3))# Output:
3.508
약 3.508이라는 값의 모평균을 얻을 수 있었다.
자, 이제 표본을 꾸려보자. 표본은 크기가 30인 배열(주사위를 30번 던진 결과)을 10개, 30개, 100개 순서로 뽑아서 표본평균 확인해 보자.
- 30번 던진 주사위 결과를 10개 표집
import random
dices_30times_10 = []
for i in range(10):
dices_30times_10.append([random.randrange(1,7) for i in range(30)])len(dices_30times_10) # 10
len(dices_30times_10[0]) # 30
표본 배열 10개의 평균 분포
자 이제 10번의 표본 평균을 구할 수 있게 되었다. 표본의 평균을 그래프로 나타내어보자.
import seaborn as sns
graph = []
for i in dices_30times_10:
graph.append(sum(i)/30)
sns.histplot(graph,bins=10)
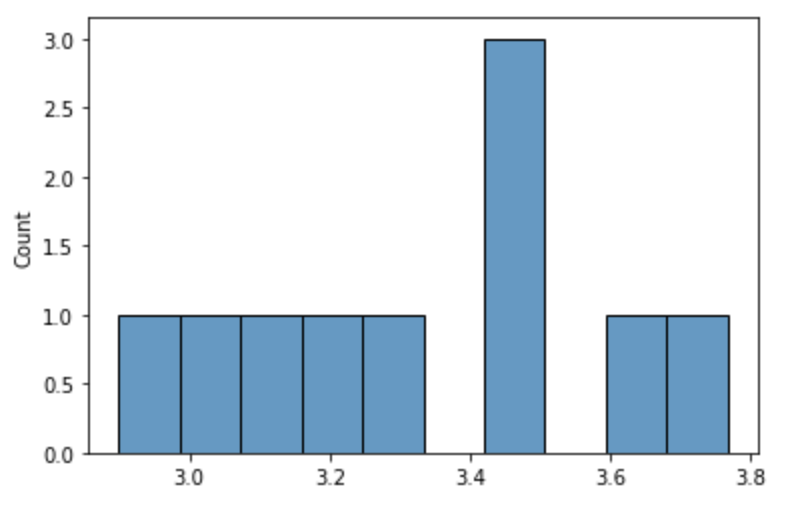
표본 배열 30개의 평균 분포
import random
dices_30times_30 = []
for i in range(30):
dices_30times_30.append([random.randrange(1,7) for i in range(30)])graph = []
for i in dices_30times_30:
graph.append(sum(i)/30)
sns.histplot(graph,bins=15)
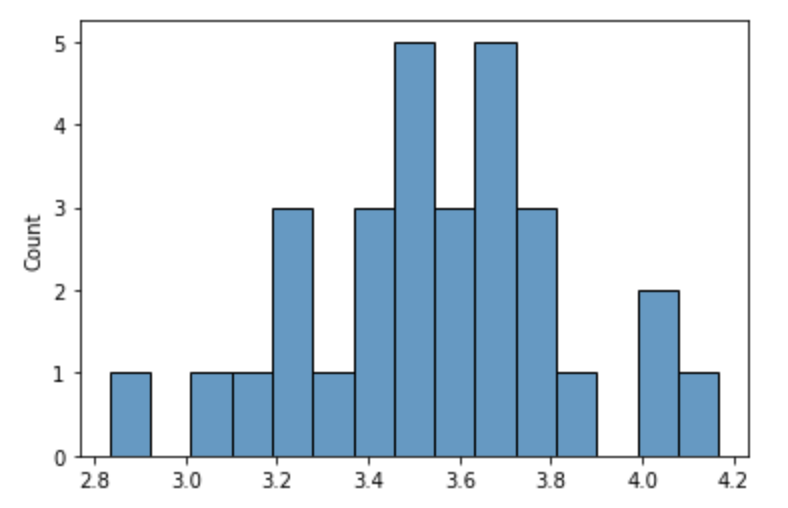
표본 배열 30개의 평균 분포
import random
dices_30times_100 = []
for i in range(100):
dices_30times_100.append([random.randrange(1,7) for i in range(30)])graph = []
for i in dices_30times_100:
graph.append(sum(i)/30)
sns.histplot(graph,bins=50)

정규분포 닮았죠?
굿.
사실, 생각하면 당연한 결과이다.
1 ~ 6 사이의 값이 독립으로 시행되는 2개의 주사위를 생각해보면 다음 표와 같다.
| ONE | TWO | THR | FOU | FIV | SIX | |
| ONE | 2 | 3 | 4 | 5 | 6 | 7 |
| TWO | 3 | 4 | 5 | 6 | 7 | 8 |
| THR | 4 | 5 | 6 | 7 | 8 | 9 |
| FOU | 5 | 6 | 7 | 8 | 9 | 10 |
| FIV | 6 | 7 | 8 | 9 | 10 | 11 |
| SIX | 7 | 8 | 9 | 10 | 11 | 12 |
무작위로 표본을 표집 할 때 평균이 3.5와 비슷한 값을 가지는 표본이 많을 것이고, 1과 6을 가지는 표본은 적을 것이다.
무작위의 표본의 평균을 집계하니 정규분포의 모양을 따르는 것이다.
이러한 정규분표를 사용하여 모집단의 평균을 추정할 수 있다.
반응형
'Python' 카테고리의 다른 글
| (Python) Web Crowling 웹크롤링 (멜론 차트 TOP 100) (0) | 2024.03.10 |
|---|---|
| (Python) 모평균 검정 (t-test, ANOVA) (0) | 2024.02.28 |
| Pandas 데이터프레임 Concat(), Merge() (0) | 2024.02.26 |
| Chapter 08. Python Pandas 기초(2) (0) | 2024.02.23 |
| Chapter 07. Python Pandas 기초(1) (0) | 2024.02.23 |




